CS6220 Unsupervised Data Mining
HW2 KMEANS and Gaussian Mixtures
Make sure you check the syllabus for the due date. Please
use the notations adopted in class, even if the problem is stated
in the book using a different notation.
We are not looking for very long answers (if you find yourself
writing more than one or two pages of typed text per problem, you
are probably on the wrong track). Try to be concise; also keep in
mind that good ideas and explanations matter more than exact
details.
Submit all code files Dropbox (create folder HW1 or similar
name). Results can be pdf or txt files, including plots/tabels if
any.
"Paper" exercises: submit using Dropbox as pdf, either typed or
scanned handwritten.
DATATSET : SpamBase: emails (54-feature vectors) classified as spam/nospam
DATATSET : 20 NewsGroups : news articles
DATATSET : MNIST : 28x28 digit B/W images
DATATSET : FASHION : 28x28 B/W images
https://en.wikipedia.org/wiki/MNIST_database
http://yann.lecun.com/exdb/mnist/
https://www.kaggle.com/zalando-research/fashionmnist
PROBLEM 1: KMeans Theory
Given Kmeans Objective discussed in class with Euclidian distance
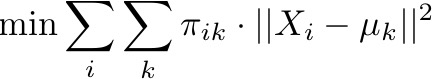
A) prove that E step update on membership (\pi) achieves the minimum objective given the current centroids( \mu)
B) prove that M step update on centroids (\mu) achieves the minimum objective given the current memberships( \pi)
C) Explain why KMeans has to stop (converge), but not necessarily to the global minimum objective value.
PROBLEM 2 : KMeans on data
Using Euclidian distance or dot product similarity (choose one per dataset, you can try other similarity metrics).
A) run KMeans on the MNIST Dataset, try K=10
B) run KMeans on the FASHION Dataset, try K=10
C) run KMeans on the 20NG Dataset, try K=20
You can use a library for distance/similarity but you have to implement your own kmeans (EM steps, termination criteria etc).
For all three datasets, evaluate the KMeans objective for a higher K (for example double) or smaller K(for example half).
For all three datasets, evaluate external clustering performance using data labels and performance metrics Purity and Gini Index (see [A] book section 6.9.2).
D) run soft Kmeans for MNIST dataset, use K=10. You can try beta=0.1, beta=1, beta=10. Evaluate performance.
PROBLEM 3 : Gaussian Mixture on toy data
You are required to implemet the main EM loop, but can use math API/functions provided by your language to calculate normal densities, covariance matrix, etc.
A) The gaussian 2-dim data on file 2gaussian.txt
has been generated using a mixture of two Gaussians,
each 2-dim, with the parameters below. Run the EM algorithm
with random initial values to recover the parameters.
mean_1 [3,3]); cov_1 =
[[1,0],[0,3]]; n1=2000 points
mean_2 =[7,4]; cov_2 =
[[1,0.5],[0.5,1]]; ; n2=4000 points
You should obtain a result visually like
this (you dont necessarily have to plot it)
B) Same problem for 2-dim data on file 3gaussian.txt , generated using a mixture
of three Gaussians. Verify your findings against the true
parameters used generate the data below.
mean_1 = [3,3] ; cov_1 =
[[1,0],[0,3]]; n1=2000
mean_2 = [7,4] ; cov_2 =
[[1,0.5],[0.5,1]] ; n2=3000
mean_3 = [5,7] ; cov_3 =
[[1,0.2],[0.2,1]] ); n3=5000
Additional notes helpful for implementing Gaussian Mixtures:
https://xcorr.net/2008/06/11/log-determinant-of-positive-definite-matrices-in-matlab/
http://andrewgelman.com/2016/06/11/log-sum-of-exponentials/
https://hips.seas.harvard.edu/blog/2013/01/09/computing-log-sum-exp/
PROBLEM 4 EM for coin flips
Three coins A,B,C with head-prob p_A, p_B, p_C can be chosen for each of N sessions. Once a coin is chosen for the session, that coin is flipped D times.
For D=20 and N=50, and fixed non-uniform selection coin probabilities pi_A, pi_B, pi_C, which sum to 1, we have this outcome , each row corresponds to a session with 20 binary 1=head 0=tail.
Compute the probabilities to select each coin to session (3 mixture "pi" probabilities), and also the bias probabilities (3 param "p" probabilities).
HINT: for each session, since the D flips are independent of each other, what matters is the number of heads out of the batch size D. If chance of head is p_ for each flip, then probability of observing x heads is binomial(x|p_, D). Here is a technical brief note .
In English: binomial(X|p_,D) = probability to get x heads out of D coin flips, if coin has head-bias p_.
PROBLEM 5 [optional, no credit] : Gaussian Mixture on real data
Run EM to obtain a Gaussian Mixture on FASHION dataset (probably won't work) and on SPAMBASE dataset (should work). Use a library/package (such as scikit-learn) and at first use the option that imposes a diagonal covariance matrix. Sampling data might be necessary to complete the run.
Supervised GDA. Train a different GMM for each label (separately on train points with that label); each GMM with small K. For testing points x, apply each GMM(x) and Bayes theorem to obtain the label with max posterior probability. Evaluate with accuracy on test data.