1. Players in a game
A friend of yours is trying to create a simple game. The game consists of players and teams. A team is made up of a collection of players.
All players have a name and a value to denote their strength. Here is the code for Player that your
friend has created.
/**
* Represents a player in the zombie game
*/
public class Player {
private String name;
private Integer strength;
public Player(String name, Integer strength) {
super();
this.name = name;
this.strength = strength;
}
/**
* @return this Player's name
*/
public String getName() {
return this.name;
}
/**
* @param name the name to set
*/
public void setName(String name) {
this.name = name;
}
/**
* @return this Player's strength
*/
public Integer getStrength() {
return this.strength;
}
/**
* @param strength
* the strength to set
*/
public void setStrength(Integer strength) {
this.strength = strength;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = (prime * result) + ((this.name == null) ? 0 : this.name.hashCode());
result = (prime * result) + ((this.strength == null) ? 0 : this.strength.hashCode());
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj) {
return true;
}
if (obj == null) {
return false;
}
if (getClass() != obj.getClass()) {
return false;
}
Player other = (Player) obj;
if (this.name == null) {
if (other.name != null) {
return false;
}
} else if (!this.name.equals(other.name)) {
return false;
}
if (this.strength == null) {
if (other.strength != null) {
return false;
}
} else if (!this.strength.equals(other.strength)) {
return false;
}
return true;
}
@Override
public String toString() {
return "Player [name=" + this.name + ", strength=" + this.strength + "]";
}
}Your friend has attempted to create a class to represent a Team but they are stuck.
/**
* Represents a team of players in the game
*/
public class Team {
private PlayerList members;
/**
* @param members
*/
public Team(PlayerList members) {
this.members = members;
}
/**
* @return this Platoon's members
*/
public PlayerList getMembers() {
return this.members;
}
/**
* @param members
* the members to set
*/
public void setMembers(PlayerList members) {
this.members = members;
}
/**
* Decreases the strengh of each player by {@code damage} units.
*
* @param damage units to decrease each players strength
*/
public void takeHit(Integer damage) {
// loop over members and decrease their
// strength by damage.
// Also if any player gets strength 0 or
// less than 0 remove them from the list
}
/**
* Increase the strengh of each player by {@code boost} units.
*
* @param boost units to increase each players strength
*/
public void takeBoost(Integer boost) {
// loop over members and increase their
// strength by boost.
}
}They have not designed PlayerLists yet. They do however feel strongly about
having the methods takeHit and takeBoost be void methods that update the
members of the team using mutation.
2. Arrays as Matrices
A startup company is building a library for manipulating matrices. They are experimenting with how to capture the design of a matrix and they hired different teams to implement these ideas so that they can compare.
You are one of those teams. Your team has been assigned one of the designs that maps a matrix to a 2-dimensional array.
The company is asking you to create a library that will implement operations on matrices. What they want is a class MatrixUtils
that will contain a set of static methods that will perform the following operations on matrices.
-
Integer[][] constantMultiplication(Integer[][] matrix, Integer const). This operation multiplies each element ofmatrixbyconst. -
Integer[][] add(Integer[][] matrixA, Integer[][] matrixB). This operations adds two matrices together, i.e.,matrixA + matrixB. The matrices must have the same dimensions in order for the operation to succeed. You can read up on matrix addition for all the relevant details. Here are some examples\[\begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix} + \begin{bmatrix} 10 \\ 20 \\ 30 \\ \end{bmatrix} = \begin{bmatrix} 11 \\ 22 \\ 33 \\ \end{bmatrix}\]\[\begin{bmatrix} 1 & 2 \\ 2 & 3\\ 3 & 4\\ \end{bmatrix} + \begin{bmatrix} 10 & 100\\ 20 & 200\\ 30 & 300\\ \end{bmatrix} = \begin{bmatrix} 11& 102 \\ 22& 203 \\ 33& 304 \\ \end{bmatrix}\]\[\begin{bmatrix} 1 & 2 \\ 2 & 3\\ 3 & 4\\ \end{bmatrix} + \begin{bmatrix} 100\\ 200\\ 300\\ \end{bmatrix} = \textrm{Error}\]\[\begin{bmatrix} 1 \\ 2\\ 3\\ \end{bmatrix} + \begin{bmatrix} 100\\ 200\\ 300\\ 400\\ \end{bmatrix} = \textrm{Error}\] -
Integer[][] transpose(Integer[][] matrixA). This operations transposes the matrix.
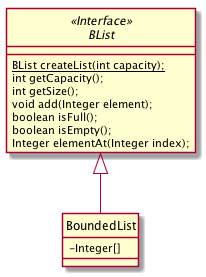
3. Bounded List
We would like to create a bounded list of Integer s called Blist. A list that has a fixed number of elements. Here are the operations that we would like to support
for our bounded list
-
BList createList(int capacity): creates a new list that can hold at mostcapacitynumber of elements. -
int getCapacity(): returns this lists capacity -
int getSize(): returns the number of non-nullelements currently in the list, a list can have 3 elements and a capacity of 10. -
boolean isFull(): returns true ifgetSize() == getCapacity() -
boolean isEmpty(): returns true if our list has no elements -
Integer elementAt(Integer index): returns the element found atindex. If the index is out of bounds this should signal an error -
void add(Integer element): add the givenelementto the next empty index in the list if we have available capacity.elementmust not benull. If the list is full signal an error.
A classmate of yours has started working on implementing BList but they are stuck. Here is their UML class diagram
3.1. Extending Bounded List
We would like to extend our bounded list implementation to provide for a method that will allow us to remove an element at a given index.
-
void removeElementAt(Integer index): remove the element at the specified index. If the index is out of bounds signal an error.
Given that our implementation uses an array, we would also like our implementation of removeElementAt to not allow for gaps
in our array after removal of an element. For example, let’s say we have a bounded list with the following contents
[1,2,3,4]
And we then perform a removeElementAt(1). If we simple remove the element at index 1 we get
[1,null,3,4]
We do not want to have gaps that contain the null value after removal. Instead our implementation should "pack" the elements
in order to avoid gaps. So our implementation should update our bounded list to be
[1,3,4,null]
3.2. Adding more capacity when needed
Lastly we would like to extend our Bounded List implementation so that if we are in the case where our list is full and we call
add instead of signalling an error we would like to first
-
increase the capacity of our list by doubling it
-
create a new array that can hold double the number of elements than our current array
-
copy all the elements in our current array into our new array keeping their index the same
-
add the new element at the next available slot in our array
So diagramatically, if we have
[1,2,3,4]
and we call add(5) we should update our bounded list implementation to be
[1,2,3,4,5,null,null,null]