 Caption:
Caption:
Context:
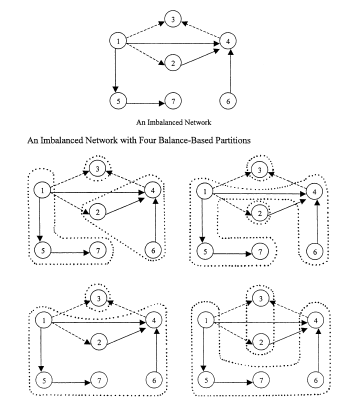
Fig. 2 presents a simple network that is not exactly balanced
together with four partitions of this network into two and three
clusters. These partitions, each with a single inconsistency with
perfect balance, were located by using the Doreian and Mrvar
(1996) method. Consider the two cluster partitions. For the
partition {{1, 2, 4, 5, 6, 7}, {3}} in the bottom-left panel in
Fig. 2, the tie from actor 1 to actor 2 is inconsistent with
balance because it is a negative tie within a plus-set. For the
partition {{1, 4, 5, 6, 7}, {2, 3}} in the bottom-right panel of
Fig. 2, the tie from actor 2 to actor 4 is identified as
inconsistent with balance because it is a positive tie between
plus-sets. We note that the tie identified in this fashion
depends on which (optimal) partition is considered. When we turn
our attention to three cluster partitions there are another two
partitions with the same number of inconsistencies with balance.
For {{1, 5, 7}, {2, 4, 6}, {3}} partition in the top-left panel
of Fig. 2, yet another tie is identified as being inconsistent
with balance. It is the positive tie from actor 1 to actor 4 that
goes between plus-sets. For the partition {{1, 4, 5, 6, 7}, {2},
{3}} in the top-right panel of Fig. 2, the positive tie from
actor 2 to actor 4 is identified again as inconsistent with
balance.
To focus our discussion, consider actor 1 and the bottom-left partition of Fig. 2 as actor 1's perception of the structure. Actor 1 has one option for generating a balanced structure in its image of the network: change the negative tie to actor 2 into a positive tie. If actor 1's perception is the lower-right partition in Fig. 2, the actor has one option: change the positive tie to actor 4 into a negative tie. Actor 1 cannot do anything about the positive tie from actor 2 to actor 4, except recognize it (or not). If actor 2 perceives either the top- or bottom-right partition of Fig. 2 as the group structure, that actor's option is to change its positive tie to actor 4 to a negative tie in an effort to reach balance. Each of these changes, even though they are instances of the same generative process, they lead to distinct collective outcomes when expressed in terms of partitioned structures.
Abstract:
Structural (or social) balance is regarded as a fundamental
social process. It has been used to explain how the feelings,
attitudes and beliefs, which the social actors have towards each
other, promotes the formation of stable (but not necessarily
conflict free) social groups. While balance theory has a rich and
long history, it has lost favor in recent times. The empirical
work has taken one of two forms. Most empirical work on social
balance has focused on dyads and triples, and findings have been
inconsistent. The remaining studies focus on the structure of the
group as a whole. Results here have been inconsistent also. One
major problem is that the first line of work is based only on the
source ideas of Heider while the second has been based only on
the ideas of Cartwright and Harary. Some of the inconsistencies
may be due to this empirical split where the two streams of ideas
do not inform each other. We propose a new theoretical model for
social balance in the form of an agent-based simulation model.
The results we present account for several of the inconsistencies
found in the literature. The model simulates distinct but
interdependent social actors making positive and negative
selections of each other in efforts to reach balanced cognitive
states. The design variables for the simulations are group size,
degree of contentiousness of a group and the mode of
communicating choices regarding the existence and sign of social
ties. The group level balance mechanism used by the dynamic model
is based on the idea of partition balance, as proposed by Doreian
and Mrvar [Soc. Netw. 18 (1996) 149]. Actor selections, over
time, generate networks that partition group members into stable,
balanced subsets at equilibrium or near equilibrium. The design
variables have complicated impacts on the number of actor choices
made to reach balance, the level of group imbalance, the number
of actors with balanced images and the number of plus-sets
formed.
Source:
Norman P. Hummon and Patrick Doreian, "Some dynamics of
social balance processes: bringing Heider back into balance
theory," Social Networks, Volume 25, Issue 1, Pages 17-49
(January 2003)