Problem Set 1
Purpose The purpose of this problem set is to remind you of the pattern-matching skills that your elementary-school teachers tried to teach you and to get you to “play” with BSL and DrRacket.
Finger Exercises Run a program from the HtDP/2e Prologue. Modify it and watch how its behaviors changes. HtDP/2e: exercises 1, 2, 3, 5, 7, 9, 10.
This is the only problem set to be completed without a partner. You will submit your homework as a single Racket file via Blackboard, before 11:59PM Friday Sep. 18. For problems that require you to define functions (problems 1 and 5), you should write actual BSL code. For the other problems, write your answers as BSL comments,
;; like this.
In these assignments, functions names like string-append are often blue, clickable links —
those links will take you to the documentation for that function, where you’ll find information about the function and examples of how to use it...along with many other related functions that might be useful too.
> (string-append "hello" " " "world") "hello world"
Develop the function thanks. It accepts a string and returns a thank you, prefixing the given name with "Thank You, " and concluding the string with an exclamation point. Thus, (thanks "Santa") produces "Thank You, Santa!" as the result.
Problem 2 You suffer from slinkies. Every night the faceless old woman who lives in your house pushes a slinky down the stairs. The faceless old woman is busy rearranging your belongings until late at night. Once she decides to take out the slinky it takes her 30 seconds to properly position it at the top of the stairs. Once the slinky begins moving it takes 7 seconds to slink from one step and the next.
Time zero represents the time that the faceless old woman loses interest in rearranging. Before 30 seconds have passed the slinky is on ‘stair 0.’ At 30 seconds the slinky starts its journey on stair 1. For every 7 seconds that pass the slinky has reached a new step. A slinky is always on one step or the next, there is no such thing as a non integer step. (Thus at time 34 the slinky is still consider to be ‘on’ stair 1. At 37 seconds the slinky is on stair 2.)
What step is the slinky on 42 seconds after the faceless old woman loses interest in rearranging? After 54 seconds?
Make a table that shows the stair the slinky will be on after 25, 35, 45, ..., 125 seconds.
Create a formula for the stair the slinky is on based on the number of seconds which have passed. Use the formula to determine what step the slinky is on after 1 hour assuming you have an infinitely long staircase.
Your submitted answer should include which steps the slinky is on at each of the requested times, the table, and the formula.
Use DrRacket’s interaction area as a calculator.
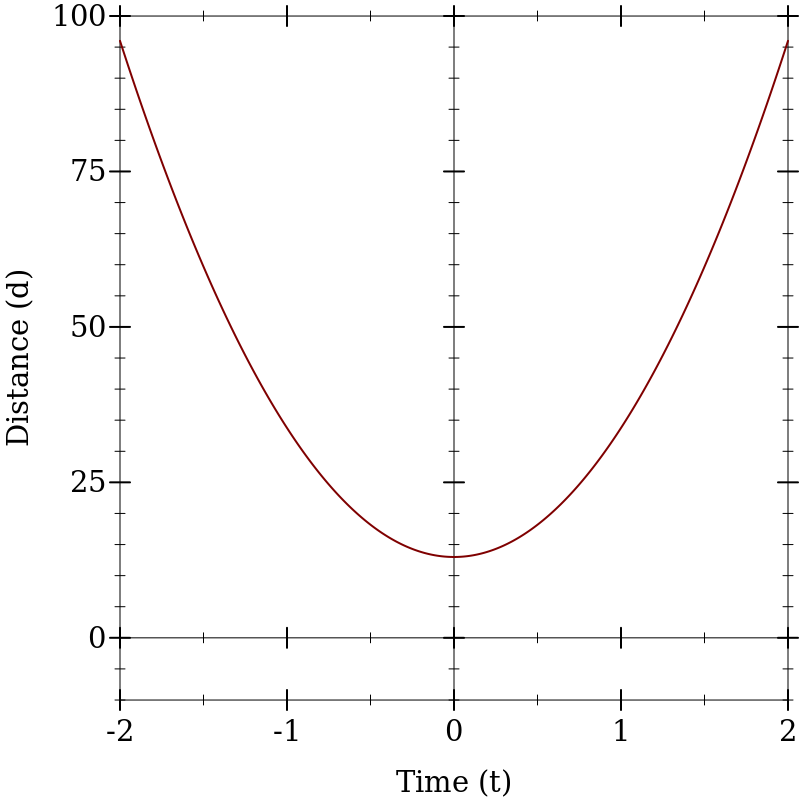
Problem 3 A pool player throws a ball on a pool table, and it then happens to roll along the diagonal. Someone films the action and then measures the ball’s trip:
after t =
0
1
2
3
4
s
it has traveled d =
13
33.75
96.0
199.75
345.0
cm
Develop a formula that calculates how far the ball gets in t seconds. Check the formula for the first five entries in the above table. If it doesn’t work, work harder. When it works, figure out how far the ball gets in 6s.
Your submitted answer should include the formula, and the position at the requested time.
Hint As discussed in class, functions come with many representations: tables, graphs, rules (formula), and so on. Here you are given a (partial) table, and your task is to guess a rule that explains how far the ball gets in t seconds. One way to guess such formulas is to switch representations. Here you could go from a table to a graph:
(+ (* a t t) b)
Use DrRacket’s interaction area as a calculator.
They pay a base fee of $10 per week just for her to be around if she is needed and $4 per container that needs to be handled.
Your submitted answer should simply be this formula, expressed as text or as a BSL function.
Use DrRacket’s interaction area as a calculator.
Problem 5 In BSL, you can create all kinds of shapes:
> (require 2htdp/image) > (star 12 "solid" "red")
> (circle 25 "outline" "green")
> (magic-wand "purple")
Ok, that last one isn’t actually built in to BSL! Develop the function magic-wand. It accepts a color string and returns an image of a magic wand: a 5-cornered star of radius 15 of that color, at the end of a black rectangle of width 40 and height 5. Use the documentation for the image library to find other image functions that may help you.